The Shunting Yard algorithm
Table of Contents
Shunting Expressions #
Foreword #
In my journey writing a book about compilers, I set out to integrate the Shunting Yard algorithm into my parser. During my research, I encountered a surprising lack of clear, practical examples, especially those addressing the challenges of handling unary operators and functions with variable arity. To fill this gap, I developed my own adaptation of the algorithm, tailored specifically to these needs. In the following sections, I’m excited to share my approach and insights. In the code examples below, we assume that we already have a working lexer producing a stream of Token variants.
The Shunting Yard algorithm #
The Shunting Yard algorithm is an ingenious method for parsing arithmetic and logical expressions written in infix notation. Originally devised by Edsger Dijkstra, the algorithm converts infix expressions into postfix notation (also known as Reverse Polish Notation) or an Abstract Syntax Tree. Its name evokes the image of a railroad shunting yard, as the process of rearranging the operators mirrors the organization of train cars. Central to its operation is its use of a stack structure, which underpins the algorithm’s efficiency and simplicity.
Infix Notation #
Infix notation is the standard format for mathematical expressions, think 3 + 4 or 5 * 10 / (2 + 3). In order to convert infix expressions into a form that a computer can evaluate more directly, the algorithm processes two streams: one for input and another for output. In addition, an operator stack temporarily holds operators until they are ready to be transferred to the output queue. This method of managing operators was a key inspiration for later developments in parsing, ultimately contributing to the operator-precedence parsing technique used in early C compilers.
A Simple Conversion to RPN #
Say we are given a string 3 * 4 + 1 which we want to convert to RPN. The algorithm goes as follows:
- Input
3 * 4 + 1 - Process “3” Push operand
3to the output queue - Process “*” Push operator
*to the operator stack - Process “4” Push operand
4to the output queue - Process “+” Push
+to the operator stack- The precedence of
+is lower than*, thus pop*of the stack and push to output - Push
+to the operator stack
- The precedence of
- Process 1 Push
1to the output queue - Final Step Pop all operators from the stack and push to output queue, in this case only
+ - Output:
34*1+
This already shows us a couple of rules:
- All operands are pushed to the output when read
- All operators are pushed to the operator stack
- If the operator at the top of the stack has a higher precedence than the current operator, we pop it and push it to the output queue
- At the end of reading the expression, pop all operators off the stack and onto the output
A graphical illustration of the algorithm, using a three-way railroad junction: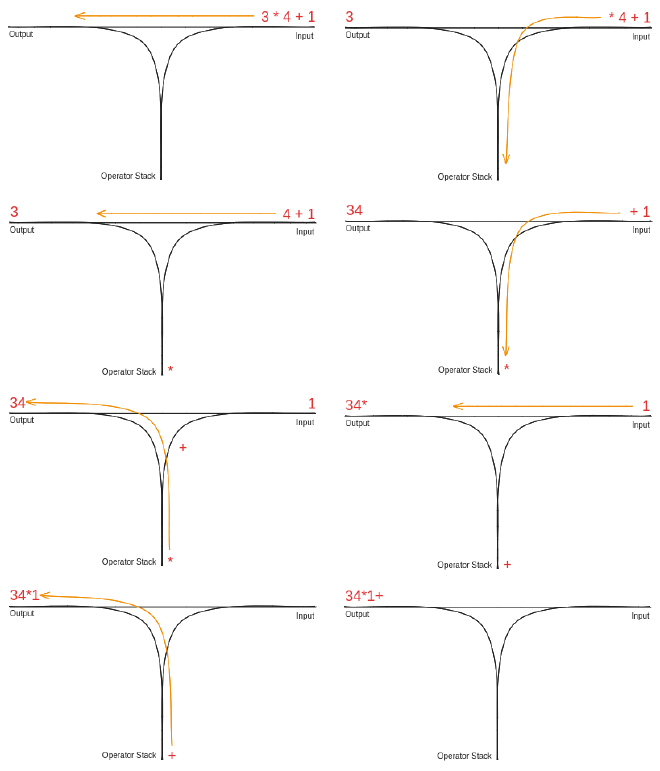
The Algorithm #
Below is pseudocode for a simple Shunting Yard algorithm, without support for unary operators or functions.
initialize output queue
initialize operator stack
while there are tokens to read:
read a token
if the token is:
- a number:
push into output queue
- an operator o1
while (
there is an operator o2 on top of the stack which is not a "("
and (
o2 has greater precedence than o1
or o1 and o2 have same precedence and o1 is left-associative
)
):
pop o2 from the stack into the output queue
push o1 onto the operator stack
- a left paranthesis ie "("
push it onto the operator stack
- a right paranthesis ie ")"
while (
the operator on top of the stack is not a "("
):
{assert the stack is not empty}
pop operator from the stack into the output queue
{assert there is a "(" at the top of the stack}
pop the left parenthesis from the stack and discard it
while there are tokens on the operator stack:
{assert the operator is not a "("}
pop the operator from the stack into the output queue
Implementation #
Let’s see how we would now implement such algorithm in my favorite language, Rust. Assume we have a Token enum that contains variants such as Integer to represent numbers, Identifier to represent variables and function names, operators and more. Our function will return a new vector containing the tokens into postfix notation. Below I will explain how you can easily extend this to return an AST instead.
fn shunting_yard<'a, T>(tokens: T) -> Vec<&'a Token>
where
T: IntoIterator<Item = &'a Token>,
{
let mut op_stack = vec![]; // Initiate our operator stack
let mut out = vec![]; // Initiate our output queue
let mut tokens = tokens.into_iter().peekable();
// While there are tokens to read, handle them
while let Some(tok) = tokens.next() {
match tok {
_ => todo!()
}
tokens = &tokens[1..];
}
// While there are operators left on the stack, push them to output
while let Some(op) = op_stack.pop() {
out.push(op);
}
out
}
Let’s now handle each match arm appropriately. We’ll assume our Token enum has a is_op() method that returns a boolean if said token is an operator or not. We’ll also assume that Token has both a get_prec() and get_assoc() method that return the precedence of the operator and associativity (in an enum) of said operator, you might panic if these methods are called on non-operator tokens.
In this case associativity refers to how operators of the same precedence are handled. For example + would be left associative as 1 + 2 + 3 would be parsed as (1 + 2) + 3, while ^ (exponentiation) would be right associative as 1 ^ 2 ^ 3 should be parsed as 1 ^ (2 ^ 3).
fn shunting_yard<'a, T>(tokens: T) -> Vec<&'a Token>
where
T: IntoIterator<Item = &'a Token>,
{
use Token::*;
let mut op_stack = vec![]; // Initiate our operator stack
let mut out = vec![]; // Initiate our output queue
let mut tokens = tokens.into_iter().peekable();
// While there are tokens to read, handle them
while let Some(tok) = tokens.next() {
match tok {
Integer(_) => out.push(tok), // Push integers to the stack
LParen => op_stack.push(tok), // Push "(" to the op_stack
RParen => {
while !matches!(op_stack.last(), Some(LParen)) {
if let Some(ref op) = op_stack.pop() {
out.push(op);
} else {
panic!("Mismatched parentheses!");
}
}
if !matches!(op_stack.last(), Some(LParen)) {
panic!("Mismatched parentheses!");
}
op_stack.pop();
}
_ if tok.is_op() => {
// Check if there are operators on op_stack with
// greater precedence
while let Some(top_op) = op_stack.last().cloned() {
if top_op.get_prec() > tok.get_prec()
|| (top_op.get_prec() == tok.get_prec() && tok.get_assoc() == Assoc::Left)
{
op_stack.pop();
out.push(top_op);
} else {
break;
}
}
op_stack.push(tok);
}
_ => todo!(),
}
tokens = &tokens[1..];
}
// While there are operators left on the stack, push them to output
while let Some(op) = op_stack.pop() {
if matches!(op, LParen) {
panic!("Mismatched parentheses at the end of input!");
}
out.push(op);
}
out
}
This algorithm perfectly handles most expressions. But what if we introduce functions? Or what about unary operators? We’ll get to that later in this post.
Complexity #
To determine the complexity of the algorithm, one has to only note that each token will be read once, each operand or operator will be pushed onto the output queue once and each operator will be pushed and popped of the stack once. Therefore there are at most a constant amount of operations for each token, resulting in a running time of \(\mathcal{O}(n)\). The algorithm is thus linear in the size of its input.
Abstract Syntax Trees #
An operator-precedence parser is a bottom-up parser and is commonly used in calculators or compilers to convert human-readable infix relying on order of operations to a format that is optimized for evaluation such as an AST. The Shunting Yard algorithm is commonly used to implement such parsers.
A simple adjustment to our algorithm can be made to produce an AST. Whenever we pop an operator from the stack, we pop the required amount of operands from the output queue and join them with the operator in a node. When the algorithm is finished, we should be left with a singular node in the output queue, our root node. If our output queue contains more than one value, the input expression was not a valid expression. And an error can be thrown.
Unary Operators #
We might also want to handle expressions such as -5 * (3 + 1), one way to do this would be to tokenize such expression into actual binary operations like 5 * (-1) * (3 + 1). But we can also handle such operators straight in our algorithm. Like before let’s first check out the pseudocode.
initialize output queue
initialize operator stack
while there are tokens to read:
read a token
if the token is:
- a number:
push into output queue
- a left paranthesis ie "("
push it onto the operator stack
- a right paranthesis ie ")"
while (
the operator on top of the stack is not a "("
):
{assert the stack is not empty}
pop operator from the stack into the output queue
{assert there is a "(" at the top of the stack}
pop the left parenthesis from the stack and discard it
- an operator o1
if (o1 is unary):
push o1 to the operator stack
else:
while (
there is an operator o2 on top of the stack which is not a "("
and o2 is unary
):
pop o2 from the stack into the output queue
while (
there is an operator o2 on top of the stack which is not a "("
and (
o2 has greater precedence than o1
or o1 and o2 have same precedence and o1 is left-associative
)
):
pop o2 from the stack into the output queue
push o1 onto the operator stack
while there are tokens on the operator stack:
{assert the operator is not a "("}
pop the operator from the stack into the output queue
To keep the code examples we simple, we assume our Token enum has both a Minus and MinusUnary variant. You could, once again, infer this during the lexical step. Or one could opt to implement a struct that contains the Token and if it is unary or not, during the parsing step you can then infer if the token is unary based on the previous token: if there is no previous token, if it’s a left parenthesis or if it’s another operator. If you make this indirection, it’s important to work with these instead of pushing plain Tokens to the output queue.
We’ll once again assume for the implementation that the Token variant has a is_unary() property.
fn shunting_yard<'a, T>(tokens: T) -> Vec<&'a Token>
where
T: IntoIterator<Item = &'a Token>,
{
use Token::*;
let mut op_stack = vec![]; // Initiate our operator stack
let mut out = vec![]; // Initiate our output stack
let mut tokens = tokens.into_iter().peekable();
// While there are tokens to read, handle them
while let Some(tok) = tokens.next() {
match tok {
Integer(_) => out.push(tok), // Push integers to the stack
LParen => op_stack.push(tok), // Push "(" to the op_stack
RParen => {
while !matches!(op_stack.last(), Some(LParen)) {
if let Some(ref op) = op_stack.pop() {
out.push(op);
} else {
panic!("Mismatched parentheses!");
}
}
if !matches!(op_stack.last(), Some(LParen)) {
panic!("Mismatched parentheses!");
}
op_stack.pop();
}
_ if tok.is_op() => {
if tok.is_unary() {
op_stack.push(tok);
} else {
// Handle pending unary operators
while let Some(top_op) = op_stack.last().cloned() {
if matches!(top_op, LParen) {
break;
}
if top_op.is_unary() {
op_stack.pop();
out.push(top_op);
} else {
break;
}
}
// Handle pending binary operators
while let Some(top_op) = op_stack.last().cloned() {
if matches!(top_op, LParen) {
break;
}
if top_op.get_prec() > tok.get_prec()
|| (top_op.get_prec() == tok.get_prec()
&& tok.get_assoc() == Assoc::Left)
{
op_stack.pop();
out.push(top_op);
} else {
break;
}
}
op_stack.push(tok);
}
}
_ => todo!(),
}
tokens = &tokens[1..];
}
// While there are operators left on the stack, push them to output
while let Some(op) = op_stack.pop() {
if matches!(op, LParen) {
panic!("Mismatched parentheses at the end of input!");
}
out.push(op);
}
out
}
Functions #
Our expression parser is almost complete. There are two more things we may introduce, variables and functions.
We would want our parser to also handle 1+x or sin(pi). This makes it a bit more difficult as we will need to consider that functions may have more than one argument, and some functions may even have varidic arguments! Plus how do we make a distinction between a plain variable, and a function call? Let’s take a look at the pseudocode:
initialize output queue
initialize operator stack
initialize argument stack
while there are tokens to read:
read a token
if the token is:
- a number:
if (top of arg_stack is 0):
increment top of arg_stack by 1
push into output queue
- an identifier:
if (top of arg_stack is 0):
increment top of arg_stack by 1
if (there is a next token and this token is a "("):
push the token into the operator stack
push 0 to the argument stack
else:
push the token into the output queue
- a left paranthesis ie "("
push it onto the operator stack
- a right paranthesis ie ")"
while (
the operator on top of the stack is not a "("
):
{assert the stack is not empty}
pop operator from the stack into the output queue
{assert there is a "(" at the top of the stack}
pop the left parenthesis from the stack and discard it
if (there is an operator o2 on top of the stack which is an identifier):
pop number of args from argument stack
push identifier with number of args to the operator stack
- a comma:
{assert argument stack is not empty}
while (
there is an operator o2 on top of the stack which is not a "("
and o2 is unary
):
pop o2 from the stack into the output queue
while (
there is an operator o2 on top of the stack which is not a "("
and (
o2 has greater precedence than o1
or o1 and o2 have same precedence and o1 is left-associative
)
):
pop o2 from the stack into the output queue
pop number of args from argument stack
push number of args + 1 to the argument stack
- an operator o1
if (o1 is unary):
push o1 to the operator stack
else:
while (
there is an operator o2 on top of the stack which is not a "("
and o2 is unary
):
pop o2 from the stack into the output queue
while (
there is an operator o2 on top of the stack which is not a "("
and (
o2 has greater precedence than o1
or o1 and o2 have same precedence and o1 is left-associative
)
):
pop o2 from the stack into the output queue
push o1 onto the operator stack
while there are tokens on the operator stack:
{assert the operator is not a "("}
pop the operator from the stack into the output queue
When encountering an identifier we do some look-ahead to handle the case of function calls. We keep track of a stack of argument amounts so we can support nested functions eg. sin(cos(pi)). When encountering a comma we check if there are any remaining remaining operators on the stack that are not a ( and handle them accordingly, this way we support expressions inside functions, eg sin(2 * pi), for each comma we encounter we increase the current argument counter by 1. Now the problem is, how do we differentiate function calls with 0 and 1 arguments, as they don’t have a comma in their expression? We can just check, when handling an integer or identifier, that the top of the argument stack is 0, if so we increase it to 1.
When a right parenthesis is encountered, like before, we handle all the operators until we reach a left parenthesis, we then check if the top most operator on the stack is an identifier, meaning a function call. Which we then push with the coresponding argument count, this way we know how many of the previous expressions in our output queue are used in the function call. Let’s finish off our implementation:
fn shunting_yard<'a, T>(tokens: T) -> Vec<&'a Token>
where
T: IntoIterator<Item = &'a Token>,
{
use Token::*;
let mut op_stack = vec![]; // Initiate our operator stack
let mut out = vec![]; // Initiate our output stack
let mut arg_stack = vec![]; // Initiate our argument stack
let mut tokens = tokens.into_iter().peekable();
// While there are tokens to read, handle them
while let Some(tok) = tokens.next() {
match tok {
Integer(_) => {
// Differentiate between functions with 0 and 1 arguments
if let Some(last) = arg_stack.last_mut() {
if *last == 0 { *last += 1; }
}
out.push(tok)
}
Identifier { .. } => {
if let Some(last) = arg_stack.last_mut() {
if *last == 0 { *last += 1; }
}
if matches!(tokens.peek(), Some(LParen)) {
// If the next token is a "(", treat it as a function call
op_stack.push(tok);
arg_stack.push(0);
} else {
// Otherwise, treat it as an identifier
out.push(tok);
}
}
LParen => op_stack.push(tok),
RParen => {
while !matches!(op_stack.last(), Some(LParen)) {
if let Some(ref op) = op_stack.pop() {
out.push(op);
} else {
panic!("Mismatched parentheses!");
}
}
if !matches!(op_stack.last(), Some(LParen)) {
panic!("Mismatched parentheses!");
}
op_stack.pop();
// Handle function calls
if matches!(op_stack.last(), Some(Identifier(_))) {
let op = op_stack.pop().unwrap();
if let Identifier(name) = op {
// In this case we just push `name({args})` to the output queue
let arg_count = arg_stack.pop().unwrap_or(0);
name.borrow_mut().push_str(&format!("({})", arg_count));
}
out.push(op);
}
}
Comma => {
if arg_stack.is_empty() {
// You can also break here to try and recover
panic!("Unexpected comma outside of function call!");
}
// Handle pending unary operators
while let Some(top_op) = op_stack.last().cloned() {
if matches!(top_op, LParen) {
break;
}
if top_op.is_unary() {
op_stack.pop();
out.push(top_op);
} else {
break;
}
}
// Handle pending binary operators
while let Some(top_op) = op_stack.last().cloned() {
if matches!(top_op, LParen) {
break;
}
if top_op.get_prec() > tok.get_prec()
|| (top_op.get_prec() == tok.get_prec() && tok.get_assoc() == Assoc::Left)
{
op_stack.pop();
out.push(top_op);
} else {
break;
}
}
arg_stack.last_mut().map(|a| *a += 1);
}
_ if tok.is_op() => {
if tok.is_unary() {
op_stack.push(tok);
} else {
// Handle pending unary operators
while let Some(top_op) = op_stack.last().cloned() {
if matches!(top_op, LParen) {
break;
}
if top_op.is_unary() {
op_stack.pop();
out.push(top_op);
} else {
break;
}
}
// Handle pending binary operators
while let Some(top_op) = op_stack.last().cloned() {
if matches!(top_op, LParen) {
break;
}
if top_op.get_prec() > tok.get_prec()
|| (top_op.get_prec() == tok.get_prec()
&& tok.get_assoc() == Assoc::Left)
{
op_stack.pop();
out.push(top_op);
} else {
break;
}
}
op_stack.push(tok);
}
}
// We break here to try and recover if a token is encountered
// that should not be part of an expression, panicing or returning
// an error here is also fine.
_ => break,
}
tokens = &tokens[1..];
}
// While there are operators left on the stack, push them to output
while let Some(op) = op_stack.pop() {
if matches!(op, LParen) {
panic!("Mismatched parentheses at the end of input!");
}
out.push(op);
}
out
}
In this implementation we have a Identifier(RefCell<String>) variant, such that we can mutate the name of the identifier when pushing it into the output queue. Ideally you’d map these tokens into something else with more meaning instead of just returning them in a seperate order.
If you’d return an AST instead of postfix notation, when pushing a function to the output queue, you’d grab the corresponding amount of arguments form the output queue with something like out.split_off(out.len().saturating_sub(arg_stack.pop().unwrap_or(0))); which can then be used in some function node.
Ideally we’d make a helper function to handle the operators, as we reuse the same logic in two places.
Shunting Yard vs Pratt Parsers #
Shunting Yard uses two (three) simple stacks, one for operators and one for output, to enforce precedence and associativity in a single left-to-right pass, resulting in true \(\mathcal{O}(n)\) performance and minimal heap allocations. In contrast, a Pratt parser or recursive descent parser dispatches on “nud” and “led” functions via recursion (or an explicit stack), which can make it very flexible; adding or tweaking operators often means writing only a few small binding-power rules, but typically incurs more AST-node allocations and deeper call stacks. In practice, Shunting Yard is often preferable when you have a fixed set of operators and want a very predictable, allocation-light parsing step, whereas Pratt shines if you expect to evolve grammar rules frequently or need tight per-operator customization.
Conclusion #
I find the Shunting Yard algorithm to be an incredibly elegant and even fun way to parse infix expressions. In essence, it processes each token exactly once, shuttles operands immediately into the output, and uses a simple operator stack to enforce both precedence and associativity rules. Because you only push and pop each operator once, and we don’t need to allocate any extra nodes or recursive frames, the core loop runs in linear time \(\mathcal{O}(n)\), where \(n\) is the number of tokens.
In our examples above, we did not perform any heap allocations for operators or operands; the only allocations are the stacks and queue that are both \(\mathcal{O}(n)\) and an extra string allocation for function arguments (which can be avoided when parsing to AST).
In summary, if your goal is to parse arithmetic or logical expressions, especially ones that include unary operators or function calls, Shunting Yard remains a top tier choice. It’s not only fast (parsing in \(\mathcal{O}(n)\) time), but it also scales naturally to handle most common expression parsing needs. If you’re looking for a lightweight yet powerful way to turn infix tokens into either postfix notation or an AST, this algorithm is hard to beat.