↓Skip to main content
  1. Posts/

Coverage checkers

·2406 words·12 mins
Compiler Pattern Matching Software Algorithm Linear Algebra Vig
Table of Contents

Coverage checkers for pattern matching #

If you’ve used functional programming languages before, or modern languages that introduced pattern matching, like Rust, you’ve likely seen an error along the lines of: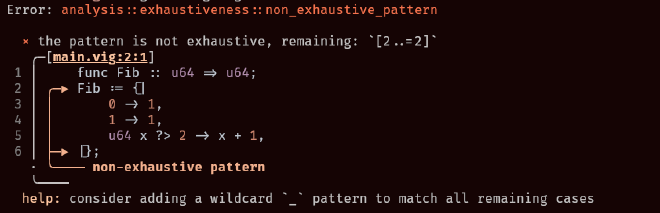

Exhaustiveness Error

For pattern matching to be safe, it’s important that every possible value of the domain has at least one pattern to match. If for example a match statement matches a bool type and only has a false arm, what would happen when we try to match true? Having the compiler catch these issues for us is thus important if we want to guarantee safety at compile time.

In this blog post we’ll take a look at the paper Rust’s coverage checker is based on, called “Warnings for pattern match”, by Luc Margaret.

What is coverage checking? #

Arity and constructors #

Assume we have some hypothetical language, a type of int has constructors 1, 2, etc with arity 0. Meaning it takes 0 arguments to construct a type of int all we have to do is take one of it’s many constructors. A type of One(_) has one constructor, namely One with an arity of 1 and a type of Cons(_,_) has one constructor with arity two.

Assume our language has three types. Nil with arity zero, One(_) with arity one and Cons(_,_) with arity two.

Pattern matrices #

The coverage checker’s job is to discover if a matrix of patterns is or is not covering all possible cases. It will also check if a specific row of patterns is useful or not given the prior rows.

Let \(P\) and \(Q\) be the following pattern matrices

$$ P = \begin{pmatrix} \text{Nil} & \text{\textunderscore} \newline \text{\textunderscore} & \text{Nil} \end{pmatrix}, \quad\quad Q = \begin{pmatrix} \text{Nil} & \text{\textunderscore} \newline \text{\textunderscore} & \text{Nil} \newline \text{One}(\text{\textunderscore}) & \text{\textunderscore} \newline \text{\textunderscore} & \text{One}(\text{\textunderscore}) \newline \text{Cons}(\text{\textunderscore}, \text{\textunderscore}) & \text{\textunderscore} \newline \text{\textunderscore} & \text{Cons}(\text{\textunderscore},\text{\textunderscore}) \end{pmatrix} $$

Let’s assume that each pattern of the matrix is of type List x = Nil | One(x) | Cons(x, List x). The above matrices correspond to the following match statements.

match x, y {
    Nil, _ => /* snip */,
    _, Nil => /* snip */,
}

match x, y {
    Nil, _ => /* snip */,
    _, Nil => /* snip */,
    One(_), _ => /* snip */,
    _, One(_) => /* snip */,
    Cons(_,_), _ => /* snip */,
    _, Cons(_,_) => /* snip */,
}

We can clearly see that \(P\) is a non-exhaustive matrix due to the lack of a One(_), _ pattern, and \(Q\) is an exhaustive matrix due to it covering all possible cases.

Usefulness #

A pattern \(q\) is useful for a matrix \(p_1,\dots,p_n\) if and only if \(q\) matches at least one case that is not matched by any pattern \(p_i\). For example, given the following matrix:

$$ P = \begin{pmatrix} \text{Nil} & \text{\textunderscore} \newline \text{Nil} & \text{One}(\text{\textunderscore}) \end{pmatrix} $$

We can clearly see that \((\text{Nil}, \text{One}(\text{\textunderscore}))\) is not useful as the earlier pattern, \((\text{Nil}, \text{\textunderscore})\), matches every single case matched by this pattern. While in the following matrix:

$$ P = \begin{pmatrix} \text{Nil} & \text{\textunderscore} \newline \text{\textunderscore} & \text{Nil} \end{pmatrix} $$

The pattern \((\text{\textunderscore}, \text{Nil})\) is useful, as it matches a new case, not matched by any preceding patterns.

Exhaustiveness #

usefulness of a pattern and the exhaustiveness of a matrix is closely related. By determining the usefulness of a particular pattern we can determine if a pattern matrix is exhaustive or not. Try to think what kind of pattern we can use to check exhaustiveness.

Consider the following pattern matrix:

$$ P = \begin{pmatrix} \text{true} \newline \text{false} \newline \text{\textunderscore} \end{pmatrix} $$

Which corresponds to the following match statement:

match x {
    true => /* snip */,
    false => /* snip */,
    _ => /* snip */
}

The wildcard pattern (_) is not useful here as every single case is already met before the wildcard is reached. The matrix is already exhausted by the presence of true and false. We can thus conclude that if the wildcard pattern is not useful the pattern matrix is exhaustive.

Exploring new values #

We now introduce two operations on the pattern matrix to recursively explore all new values a candidate pattern can match, and thus decide usefulness and, after all arms, exhaustiveness.

Assume we have the following Rust code:

enum Opt {
    None,
    Some(u64)
}

match x {
    None => /* snip */,
    Some(0) => /* snip */,
    _ => /* snip */,
}

Which corresponds to the matrix

$$ P = \begin{pmatrix} \text{None} \newline \text{Some}(0) \newline \text{\textunderscore} \end{pmatrix} $$

Specialization #

Specialization on a constructor \(c\) builds a new matrix \(S(c,P)\) by keeping only those rows whose first pattern is either \(c(…)\) or a wildcard, then “peeling off” the head. Each \(c(p_1,\dots,p_k)\) row is replaced by its subpatterns \((p_1,\dots,p_k)\) and each wildcard row spawns \(k\) wildcards (one per field of \(c\)), while all other rows are dropped. This lets us reduce an \(n-\)column problem to a \((n-1)-\)column one, focusing our usefulness check solely on the inner values of \(c\).

We then recurse on each such specialized matrix (and on the default matrix (see later) for wildcards) if any recursive call finds a “new” value that wasn’t previously covered, the original pattern is deemed useful, otherwise it’s redundant.

Let’s now look at the above example of matrix \(P\).

  1. Specialize on None

We want \(S(\text{None}, P)\) to only keep rows whose head can match None and, if the row is None we remove the None and expose the inner field, in this case an empty tuple (), if the row is _ we replace it by a wildcard of the same arity (here arity = 0).

So for row 0 we find None which matches None, we push one empty row (). For row 1 we find Some(0), so drop. And row 2 has _ push one empty row (). Thus we find that

$$ S(\text{None}, P) = \begin{pmatrix} () \newline () \end{pmatrix} $$

Which is a \(2 \times 0\) matrix, that means the pattern matrix \(P\) is fully exhaustive for the None constructor, every possible value built with the None constructor is matched in at least one row of \(P\).

Side note a non-empty \(S(c, P)\) does not by itself mean “redundant”. It simply means “there were previous rows matching constructor \(c\)”. We must recurse on the remaining columns (see later), only if this also fails can we declare the pattern redundant. But because None has arity zero, we know we don’t have to recurse and know that recursing further will yield the emptyset \(\emptyset\), meaning the pattern is redundant.
  1. Specialize on Some

In row 0 we find None, which we drop. In row 1 we find Some(0) which we decompose to it’s inner pattern (0) for row 2 we find a wildcard _ which we decompose to a wildcard of the same arity, (_). Resulting in

$$ S(\text{Some}, P) = \begin{pmatrix} (0) \newline (\text{\textunderscore}) \end{pmatrix} $$

Because \(S(\text{Some}, P)\) is non-empty, the constructor Some (and in particular patterns like Some(1)) can still match new values. So any new Some(...) arm is useful and we must recurse on that inner value (see later) to pin down exactly what values remain.

Defaulting #

  1. Defaulting on _

Finally remains \(S(\text{\textunderscore}, P)\), the “otherwise” case. We keep only the rows whose head is a wildcard and then strip it off.

In row 0 we find None which we drop, same for row 1. In row 2 we find _ so we push a () empty tuple, and find that:

$$ S(\text{\textunderscore}, P) = \begin{pmatrix} () \end{pmatrix} $$

Since \(S(\text{\textunderscore}, P)\) yielded a non-empty \(1 \times 0\) matrix, it tells us that there are values of the scrutinee whose constructor was not in the explicit arms (None or Some(0)) and those values are matched by the wildcard arm. The “otherwise” branch still has something to catch, so the wildcard arm is useful and we know there remain constructor or literal cases that haven’t yet been explicitely covered.

The algorithm #

To decide whether a candidate pattern \(q\) is useful (i.e. matches some value not already covered by a set of prior patterns \(P\)), we use the following recursive procedure:

  1. Base cases

    • if \(P\) is empty, every pattern is useful (there’s nothing covered yet)
    • if \(q\) has no columns left (we peeled off all constructors) but \(P\) is non-empty, it can’t match anything new so \(q\) is deemed not useful

  2. Look at the first column of \(q\)

    • call its head \(q_1\) and its tail \(q_{\text{tail}}\)
    • if \(q_1\) is a constructor \(c(…)\):
      1. Compute the specialized matrix \(P’=S(c,P)\)
      2. Recurse on the smaller problem \(\text{isuseful}(P’,q_{\text{tail}})\)
      3. Whatever returns is the answer
    • if \(q_1\) is a wildcard _
      1. enumerate all constructors \(c\) seen in the first column of \(P\), for each such \(c\) do:
        • Compute \(P_c=S(c,P)\)
        • Recurse on \(\text{isuseful}(P_c,q_{\text{tail}})\)
        • if any of those returns true, then \(q\) is useful
      2. if the set of seen constructors was incomplete (i.e. there exists other constructors we haven’t tested), or if none of the above recursive calls returned true, compute the default matrix \(P_{\text{\textunderscore}}=S(\text{\textunderscore}, P)\) and recurse on \(\text{isuseful}(P_{\text{\textunderscore}},q_{\text{tail}})\)
      3. if that recursive call returns true, \(q\) is useful; otherwise it’s not.

So to make it more clear, in words. To see if \(q\) can ever match a value not already matched by \(P\), we strip off its first constructor (or wildcard), carve out exactly the rows of \(P\) that could have matched the same constructor, and then we answer the same question on the remainder.

For wildcards we try every constructor seen so far, and if there are gaps an ‘otherwise’ branch, so that if any branch finds a fresh value \(q\) is declared useful; only if all recursive branches fail do we conclude \(q\) is redundant.

Show me the code #

We’ll look at a simple implementation in Rust without algebraic types. Let’s first define a Pattern enum and a Matrix type that holds our patterns.

#[derive(Debug, Clone, PartialEq, Eq)]
enum Pattern {
    Wildcard,
    Literal(i128),
}

pub type Matrix = Vec<Vec<Pattern>>;

We’ll now implement both specializing and defaulting.

pub fn specialize(matrix: &Matrix, ctor: &Pattern) -> Matrix {
    matrix
        .iter()
        .filter_map(|row| match (&row[0], ctor) {
            (Pattern::Literal(n1), Pattern::Literal(n2)) if n1 == n2 => Some(row[1..].to_vec()),
            (Pattern::Wildcard, _) => Some(row[1..].to_vec()),
            _ => None,
        })
        .collect()
}

We use a neat oneliner by converting our matrix to an iterator and using the filter_map method, which will map each value to the inner of the Some variant and remove any values that return None. We can thus simply match over \(q_1\) and the constructor and see if they are equal and map it to \(q_{\text{tail}}\). Wildcards also get mapped to \(q_{\text{tail}}\) and anything else gets discarded.

pub fn default_matrix(matrix: &Matrix) -> Matrix {
    matrix
        .iter()
        .flat_map(|row| {
            if let Pattern::Wildcard = row[0] {
                Some(row[1..].to_vec())
            } else {
                None
            }
        })
        .collect()
}

Defaulting is nearly the exact same approach, except we only map if \(q_1\) is a wildcard and drop if not.

With these two in place, we can implement the main is_useful function, which will check if a row of patterns \(q_1, \dots, q_n\) is useful or not.

pub fn is_useful(matrix: &Matrix, pat: &[Pattern]) -> bool {
    // No prior rows, pattern is useful
    if matrix.is_empty() {
        return true;
    }

    // All columns are peeled off, nothing new to match
    if pat.is_empty() {
        return false;
    }

    // Split pattern in head and tail
    let (pat_head, pat_tail) = (&pat[0], &pat[1..]);

    match &pat_head {
        // Constructor
        Pattern::Literal(c) => {
            // Specialize on the constructor and recurse with tail
            let spec = specialize(matrix, &Pattern::Literal(*c));
            is_useful(&spec, pat_tail)
        }
        // Wildcard
        Pattern::Wildcard => {
            // Find all prior constructors
            let mut seen_literals: Vec<i128> = matrix
                .iter()
                .filter_map(|row| {
                    if let Pattern::Literal(n) = row[0] {
                        Some(n)
                    } else {
                        None
                    }
                })
                .collect();
            seen_literals.sort_unstable();
            seen_literals.dedup();

            // Specialize on each constructor
            for c in seen_literals {
                let spec = specialize(matrix, &Pattern::Literal(c));
                if is_useful(&spec, pat_tail) {
                    return true;
                }
            }

            // default (the "otherwise" branch)
            let def = default_matrix(matrix);
            is_useful(&def, pat_tail)
        }
    }
}

In here we can clearly see our algorithm from earlier take form. Our two base cases at the top will deem \(q\) useful, if the pattern matrix is empty and not useful if \(q\) itself is empty.

We then split \(q\) into it’s head and tail and match the head. When \(q_1\) is a constructor, in this case our Pattern::Literal we specialize on that constructor and recursing on the tail. If \(q_1\) is a wildcard we first try each constructor that actually appears in the prior rows, and if none of those yield a new value, we form a default matrix by keeping only the wildcard rows and stripping their head and recursing on it.

This set of functions implements a basic version of the recursive “specialize & split” procedure described by Luc Maranget. We can introduce one more function which can determine all redundant arms and if a match statement is exhaustive or not all in one.

fn check_patterns(arms: &[Pattern]) -> (Vec<usize>, bool) {
    // Build a pattern matrix
    let rows: Matrix = arms.iter().map(|p| vec![p.clone()]).collect();

    let mut seen = Vec::new();
    let mut redundant = Vec::new();

    for (i, row) in rows.iter().enumerate() {
        if !is_useful(&seen, row) {
            redundant.push(i);
        }
        seen.push(row.clone());
    }

    // Check for exhaustiveness by checking if _ is useful
    let wildcard = vec![Pattern::Wildcard];
    let non_exhaustive = is_useful(&seen, &wildcard);

    (redundant, !non_exhaustive)
}

Handling Guards #

Guard’s are a vital tool in pattern matching. For example:

match x {
    0..=10 => /* snip */,
    x if x > 30 => /* snip */,
    _ => /* snip */
}

Guard’s don’t change the structure of the value being matched, they only filter it after a succesful constructor match. In practice, the coverage checker treats every guarded pattern as if it were a wildcard in the matrix recursion, then applies the guard seperately at runtime, ensuring that structural exhaustiveness remains sound without complicating the core algorithm.

Conclusion #

Pattern match coverage checking is a deceptivly simple idea, but when you support algebraic types, nested constructors and mixed wildcard/guarded patterns, the bookkeeping gets subtle. Luc Maranget’s constructor-matrix method gives us a uniform and recursive recipe:

  1. Specialize on each constructor to peel off one layer of structure
  2. Default to cover “everything else”
  3. Recurse until either you uncover a fresh value (pattern is useful) or you run out of columns (patern is redundant)

By translating this into a few small helper functions, specialize, default and is_useful, your compiler can simultaneously detect unreachable code and guarantee that every possible value is handled, all at compile time and without runtime overhead.